Unevaluating polynomials

I have a function that evaluates polynomials with integer coefficients. To evaluate $$%<![CDATA[ f(x) = 6 + 5x + 2x^3 %]]>$$ at $f(8)$, for example, you do this:

scala> evalPoly(8, List(6, 5, 0, 2))
res0: (Int, Int) = (8, 1070)

For some reason it echoes the input back out to you. Here’s the code you might write:

def evalPoly(x: Int, coeffs: List[Int]): (Int, Int) = {
  def eval(cs: List[Int]): Int = {
    cs match {
      case Nil => 0
      case h :: t => x * eval(t) + h
    }
  }
  (x, eval(coeffs))
}

This should not be surprising.

But I also have a function that un-evaluates polynomials. To un-evaluate $f(8) = 1070$, you do this:

scala> unevalPoly(8, 1070)
res1: (Int, List[Int]) = (8, List(6, 5, 0, 2))

and it echoes your input and gives you back the coefficients of the polynomial.

Wait, what? I thought you needed $N+1$ points to determine an $N$-degree polynomial. Here I’ve seemingly done it with just one point. To spoil the surprise a little, unevalPoly doesn’t always work. But how does it work even some of the time? How would you go about coding this up?

Having noticed that the input to unevalPoly is the output of evalPoly, and vice versa, one tack we can try is to write evalPoly backwards. First let me rewrite it slightly:

def evalPoly(x: Int, coeffs: List[Int]): (Int, Int) = {
  def eval(cs: List[Int]): Int = {
    cs match {
      case Nil => 0
      case h :: t => plustimes(x, eval(t), h)
    }
  }
  (x, eval(coeffs))
}

I’ve just replaced x * eval(t) + h with a call to this function:

def plustimes(n: Int, q: Int, r: Int) = {
  n * q + r
}

Now here’s eval as a data flow diagram. I’ve threaded through x as a “context” variable because it isn’t an input to eval per se.

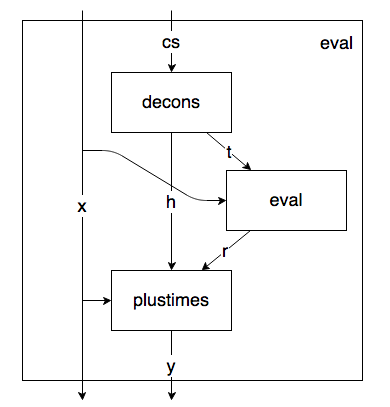
Following the arrows backwards from the outputs to the inputs we can write the following code:

def unevalPoly(x: Int, y: Int): (Int, List[Int]) = {
  def uneval(y: Int): List[Int] = {
    y match {
      case 0 => Nil
      case y => {
        val (q, r) = unplustimes(x, y)
        r :: uneval(q)
      }
    }
  }
  (x, uneval(y))
}

Now this should work as long as we can write unplustimes, which is possible only when plustimes doesn’t destroy information. So given m and n and m = n * q + r, when can we recover q and r?

Well, if r happens to be less than n, this is just like doing long division — q and r are the quotient and remainder when dividing m by n:

def unplustimes(n: Int, m: Int): (Int, Int) = {
  val q = m / n
  val r = m % n
  (q, r)
}

This works because for a given positive integer $n$, any integer $m$ can be written uniquely as $m = nq + r$, where $q$ and $r$ are nonnegative integers and $r \lt n$. Since this formulation is unique, it’s easy to reverse the process and recover $q$ and $r$.

So what does that mean for unevalPoly? It will only work if

1. x is a positive integer, and
2. all of the coefficients are nonnegative integers less than x.

Let’s try it out. This works:

scala> evalPoly(8, List(1, 3))
res0: (Int, Int) = (8, 25)

scala> unevalPoly(8, 25)
res1: (Int, List[Int]) = (8, List(1, 3))

But this doesn’t, as expected:

scala> evalPoly(2, List(1, 4, 2))
res2: (Int, Int) = (2, 17)

scala> unevalPoly(2, 17)
res3: (Int, List[Int]) = (2, List(1, 0, 0, 0, 1))

And neither does this:

scala> evalPoly(5, List(1, -2, 1))
res4: (Int, Int) = (5, 16)

scala> unevalPoly(5, 16)
res5: (Int, List[Int]) = (5, List(1, 3))

Neat though!

A puzzle

This all came to me through a puzzle I heard: Your friend has a secret polynomial, which you know has nonnegative integer coefficients. She challenges you to determine the coefficients of the polynomial, offering to evaluate the polynomial for you on any two numbers you choose.

From the above, you know need to evaluate the polynomial at a number that is larger than all of the coefficients. So all that’s left to the solution is finding some number that satisfies that description.

What’s really going on

You might have noticed that all unevalPoly(n, m) is doing is converting m to its representation in base n. Here it is converting 42 to base 2:

scala> unevalPoly(2, 42)
res6: (Int, List[Int]) = (2,List(0, 1, 0, 1, 0, 1))

And oh, look:

scala> unevalPoly(10, 12345)
res7: (Int, List[Int]) = (10, List(5, 4, 3, 2, 1))

This all makes sense now. The polynomial

is what you mean when you write $abcde_x$, which is the unique representation of that number in base $x$ provided that all of the coefficients are less than $x$. Recovering the coefficients of $f(x) = y$ is the same as writing $y$ in base $x$.

So backwards programming is good for something! If this interests you, you should read my last post on backwards sorting algorithms.